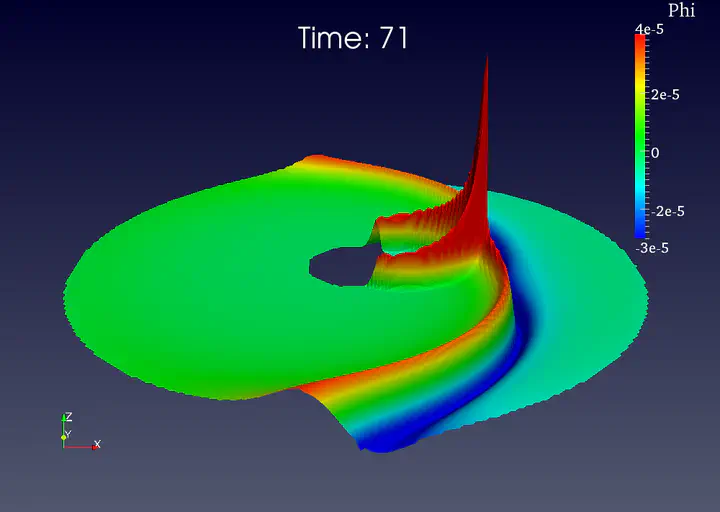
 Caustic echo #4 at $t=71M$
Caustic echo #4 at $t=71M$Abstract
Animations on YouTube for nonrotating and rotating cases.
We present the first numerical approximation of the scalar Schwarzschild Green function in the time domain, which reveals several universal features of wave propagation in black hole spacetimes. We demonstrate the trapping of energy near the photon sphere and confirm its exponential decay. The trapped wavefront passes through caustics resulting in echoes that propagate to infinity. The arrival times and the decay rate of these caustic echoes are consistent with propagation along null geodesics and the large $\ell$ limit of quasinormal modes. We show that the fourfold singularity structure of the retarded Green function is due to the well-known action of a Hilbert transform on the trapped wavefront at caustics. A twofold cycle is obtained for degenerate source-observer configurations along the caustic line, where the energy amplification increases with an inverse power of the scale of the source. Finally, we discuss the tail piece of the solution due to propagation within the light cone, up to and including null infinity, and argue that, even with ideal instruments, only a finite number of echoes can be observed. Putting these pieces together, we provide a heuristic expression that approximates the Green function with a few free parameters. Accurate calculations and approximations of the Green function are the most general way of solving for wave propagation in curved spacetimes and should be useful in a variety of studies such as the computation of the self-force on a particle.