Abstract
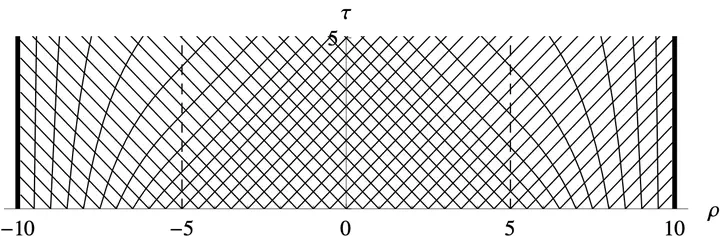
We show how to solve hyperbolic equations numerically on unbounded domains by compactification, thereby avoiding the introduction of an artificial outer boundary. The essential ingredient is a suitable transformation of the time coordinate in combination with spatial compactification. We construct a new layer method based on this idea, called the hyperboloidal layer. The method is demonstrated on numerical tests including the one dimensional Maxwell equations using finite differences and the three dimensional wave equation with and without nonlinear source terms using spectral techniques.
Type
Publication
Journal of Computational Physics