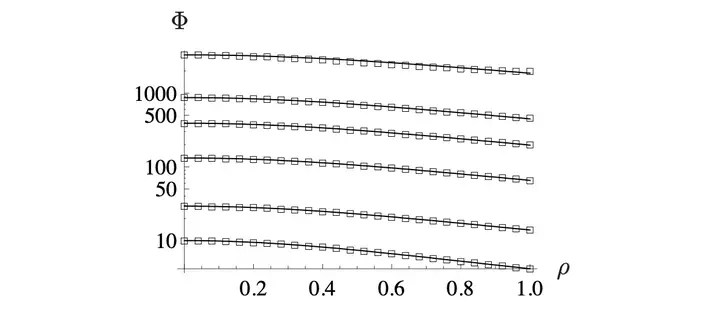
Agreement between
universal attractor and
numerical solution
during blowup at
every grid point.
First example of
global blowup
for a wave equation.
Abstract
We consider the initial value problem for the spherically symmetric, focusing cubic wave equation in three spatial dimensions. We give numerical and analytical evidence for the existence of a universal attractor which encompasses both global and blowup solutions. As a byproduct we get an explicit description of the critical behaviour at the threshold of blowup.
Type
Publication
Nonlinearity